Algorithmen mit Wiederholungen

Wiederholungsstruktur mit Anfangsbedingung

Einführungsbeispiel

Die nach Leonhard Euler benannte Eulersche Zahl e=2,718281828459... ist eine irrationale Zahl.

Die Eulersche Zahl ist die Basis des so genannten natürlichen Logarithmus. Sie spielt in der Differential- und Integralrechnung eine wichtige Rolle.

Die Zahl e kann unter anderem durch Grenzwertbildung definiert werden (eine Möglichkeit von vielen)

<

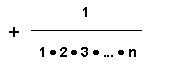 Mithilfe eines Programms soll die Eulersche Zahl  für ein bestimmtes n <17 bestimmt werden

Syntax

Die Wiederholungsanweisungen mit Anfangsbedingung ermöglicht es, eine Anweisung mehrfach auszuführen. Vor jeder Ausführung wird geprüft, ob die Schleifenbedingung noch erfüllt ist. Nur dann erfolgt eine Ausführung.

WHILE <Bedingung> DO   BEGIN  <Anweisungen> END;

Struktogramm 

Beispiel

program euler;
uses crt;

var  a, p, z :  integer;
     e       :  real;

begin
     clrscr;
     readln(a);
     if a>17 then writeln('Bitte eine kleinere Zahl eingeben')
     else
     begin
       e:=1;
       p:=1;
       z:=1;

       while z <= a do			{+++ solange z kleiner ist als a +++}
       begin				{+++ führe aus : +++}
         p := p * z;			
         e := e + 1/p;
         inc(z);			{+++ z wird um 1 erhöht+++}
         writeln((z-1):4,e:16:12);
       end;

       writeln;writeln('als Vergleich e = 2,7182818284...');
     end;
     readln;
end.